Traditionally, training methods for deep learning solutions (DL) have their roots in the principles of the human brain. In this context, neurons are represented as connected nodes, and the strength of these connections changes with the impact of neurons. Deep neural networks consist of three or more nodes, including input and output layers. However, these two learning scenarios are significantly different. First of all, effective DL architecture requires dozens of hidden supply layers, which are currently expanding to hundreds, while brain dynamics consists of only a few layers of power supply.
Secondly, deep learning architecture usually includes many hidden layers, and most of them are weaves. These weaves are looking for specific patterns or symmetry in small input data sections. Then, when these operations are repeated in subsequent hidden layers, they help identify larger features that determine the class of input data. Similar processes were observed in our visual cortex, but the approximate conditional connections were mainly confirmed from the retina entrance to the first hidden layer.
Another complex aspect of deep learning is that the technique of reverse propagation, which is crucial for the operation of neural networks, has no biological analogue. This method adapts the weight of neurons so that they become more suitable to solve the task. During the training, we provide data introduction and compare how much it differs from what we would expect. We use the error function to measure this difference.
Then we start to update the weight of neurons to reduce this error. To do this, we consider each path between the entry and exit of the network and determine how every weight on this path contributes to a general error. We use this information to correct weight.
Returning and in full combined layers of the network play a key role in this process and are particularly efficient due to parallel calculations on graphics processing units. It is worth noting, however, that such a method does not have analogues in biology and differs from how the human brain processes information.
So, although deep learning is powerful and effective, there is an algorithm developed only for machine learning and does not imitate the biological learning process.
Scientists from Bar-Ilan University in Israel wondered if it is possible to develop a more efficient form of artificial intelligence, using architecture resembling an artificial tree. In this architecture, each weight has only one path to the output unit. Their hypothesis is that this approach can lead to higher classification accuracy than in more complex architectures of deep learning, which use more layers and filters. The study was published in the journal Scientific reports.
The core of this study examines whether learning in architecture resembling a tree, inspired by dendritic trees, can achieve results as effective, as usual achieved using more structured architectures covering many fully combined and floatable layers.
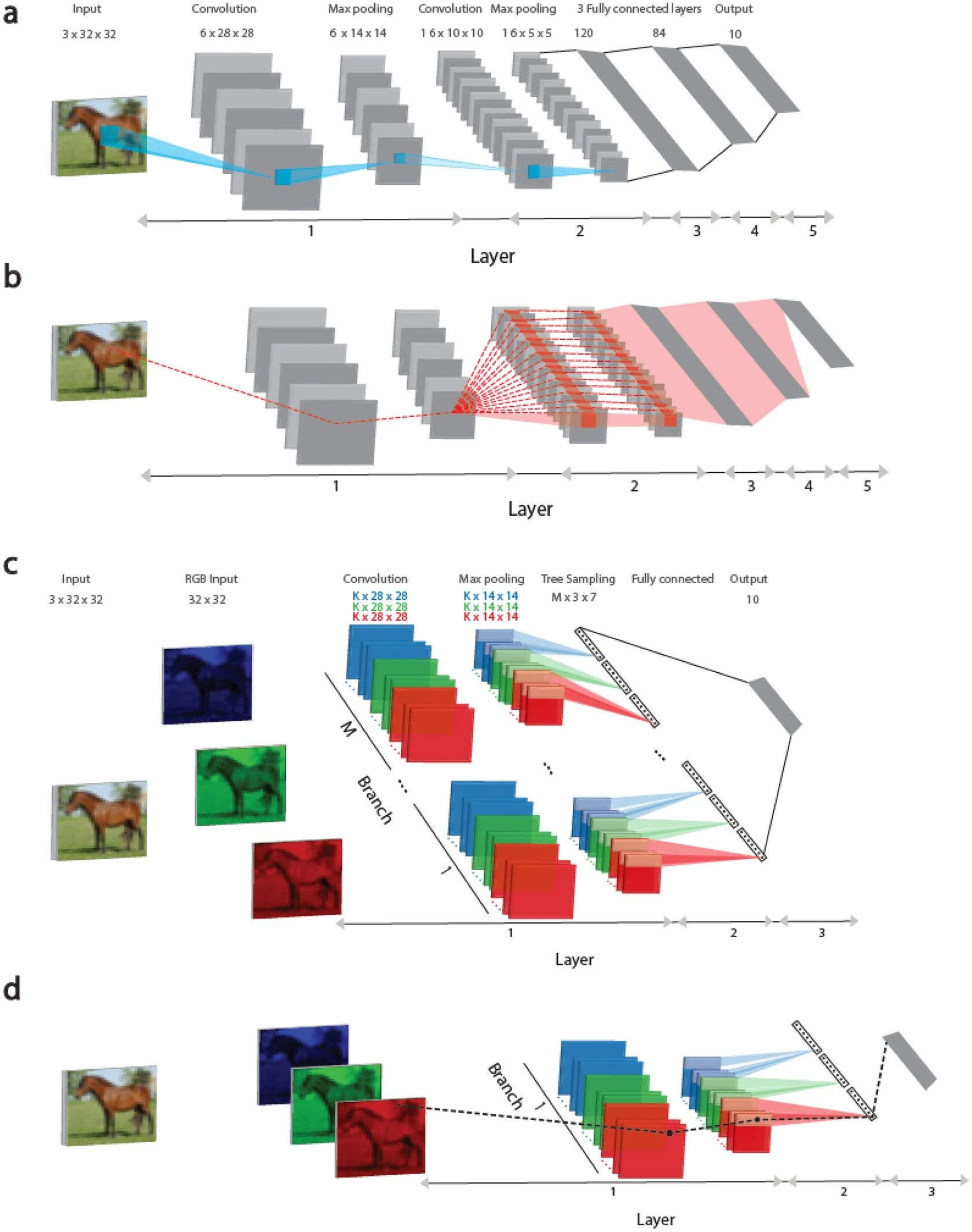
Figure 1
This study presents the learning approach based on architectures reminiscent of a tree in which each weight is connected to the output unit only one route, as shown in Figure 1 (C, D). This approach is a step closer to the realistic implementation of biological learning, taking into account Recent arrangements that dendrites (parts of neurons) and their direct branches can change, increasing the strength and expression of the signals that pass through them.
Here, it has been shown that the performance indicators of the proposed TREE-3 architecture, which has only three hidden layers, exceed the achieved Lenet-5 success indicators in the CIFAR-10 database.
Lenet-5 and Tree-3 weave architecture is considered in Figure 1. The Lenet-5 weave network for the CIFAR-10 database consists of 32 × 32 RGB input images, belonging to 10 output labels. The first layer consists of six (5 × 5) weave filters, and then (2 × 2) the maximum bullet. The second layer consists of 16 (5 × 5) weave filters, and layers 3-5 have three fully connected hidden layers of 400, 120 and 84, which are connected to 10 output units.
In Figure 1 (b), the dashed red line indicates a scheme of routes affecting the mass updates belonging to the first layer on the panel (A) during error technique at the back. The weight is connected to one of the output units by many routes (intermittent red lines) and can exceed a million. It should be noted that all weights on the first layer are identified with 6 × (5 × 5) weights, belonging to six weave filters, as shown in Figure 1 (C).
The architecture of TREE-3 consists of m = 16 branches. The first layer of each branch consists of K (6 or 15) filters (5 × 5) for each of the three RGB channels. Each channel is coupled with its own set of K filters, which gives 3 × K various filters. Filters weaves are the same for all branches of M. The first layer ends with the maximum container consisting of non -overlapping squares (2 × 2). As a result, there are (14 × 14) output units for each filter. The second layer consists of a sampling resembling a tree (not to the tactless) (2 × 2 × 7 units) of K filters for each RGB in each branch, which gives 21 output signals (7 × 3) for each branch. The third layer fully connects the output of the branches of 21 × m output modules layer 2 to 10. The reel activation function is used to learn online, while sigmoid is used to learn offline.
In Figure 1 (D), the intermittent black line means a scheme of one route connecting the updated weight on the first layer, as shown in Figure 1 (C), during the background technique of the retrospective error of the output device.
To solve the classification task, scientists used the cost of cost between entropy and used the stochastic gradient algorithm to minimize it. To refine the model, optimal hyperparameters were found, such as learning speed, constant shoot and mass breakdown coefficient. To evaluate the model, several sets of validation data consisting of 10,000 random examples similar to the set of test data were used. The average results were calculated, taking into account the standard deviation from the given average success indicators. The study uses the Nesterova method and l2 regulatory.
Offline hyperparameters, including η (learning speed), μ (constant shoot) and α (l2 regulatoryization), were optimized during offline learning, which included 200 eras. Online learning hyperparameters have been optimized using three different examples of the data set.
As a result of the experiment, an effective approach to the training of architecture resembling a tree was shown in which each weight is connected to the output unit by only one road. This is a approximation to biological learning and the ability to use deep learning with very simplified dendritic trees of one or several neurons. It should be noted that adding the weight layer to the input data helps to keep a tree similar to the tree and improve success compared to architecture without weave.
While the Lenet-5 computing complexity was much higher than in the TREE-3 architecture with comparable success rates, its efficient implementation requires new equipment. It is also expected that the training of architecture resembling a tree will minimize the likelihood of gradient explosions, which is one of the main challenges for deep learning. The introduction of parallel branches instead of the second weave in Lenenet-5 improved success indicators while maintaining a tree-like structure. Further study is justified to examine the potential for large and deeper architecture resembling trees, containing an increased number of troops and filters, in order to compete with modern indicators of the success of Cifar-10. This experiment, using the Lenet-5 as a starting point, emphasizes the potential benefits of dendritic learning and its computing capabilities.


















